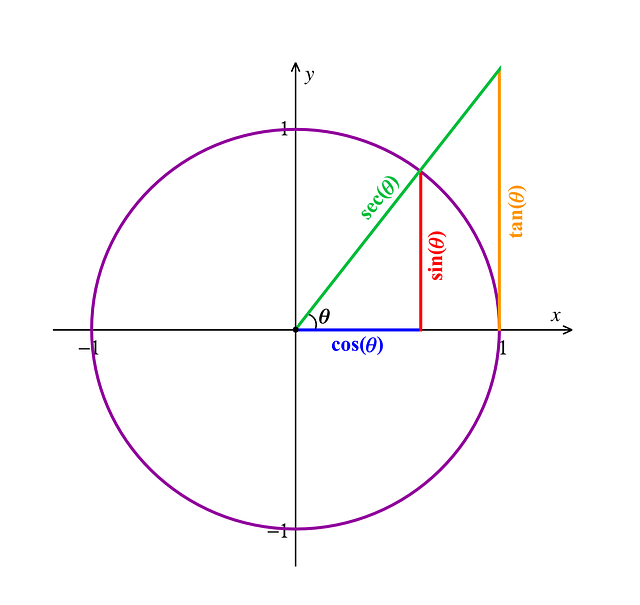
Trigonometry – A Crucial Branch of Mathematics with Real-Life Applications

Trigonometry is a branch of immense importance. Trigonometry deals with the angles and sides of a triangle. Every student and instructor needs a trigonometric tool to help them overcome issues not only in mathematics but also in other areas. Many physics derivations are impossible to complete without using trigonometry. Many identities and formulas are used in trigonometry, and a thorough understanding of them is required. Understanding the fundamentals of this topic, just like any other subject, is essential for avoiding future errors in solving difficulties. Let us discuss trigonometric ratios and identities in detail.

Trigonometric ratios: Take any two sides of a right-angled triangle to get the ratios of the sides of that triangle. These ratios are only considered trigonometric ratios. When we find all of the ratios, we come to know that in total there are six trigonometric ratios. Sine, cosine, tangent, secant, cosecant and cotangent are considered as the six trigonometric identities. By taking any of the two sides of the given right-angled triangle, we can calculate these ratios. There are specific two sides that give a particular ratio. Let us take all the six ratios and the sides required to calculate them

 

For calculating sine, we need the ratio of the perpendicular and the hypotenuse of the given triangle. For cosine, it is required to divide the base of the triangle with the hypotenuse. To get the value of tan we need to take the ratio of perpendicular and base of the triangle. To calculate the cot, divide the base by perpendicular. For a sec, divide the hypotenuse by base and at last to calculate the value of cosec, divide the hypotenuse of the triangle with the perpendicular. Apart from the above formulas, we also have reciprocal relations for all the trigonometric ratios. Let us have a look at them. Sin is reciprocal of cosec, tan is reciprocal of cot and cos is reciprocal of sec. It is important to understand the trigonometric ratios as they are the foundation of trigonometry.

 

Trigonometric identities: Whenever a trigonometry problem arises, we will almost certainly need to use trigonometric identities. The only known triangle for which these identities are defined is a right angle. Let us discuss a few of the trigonometric identities. There are ratio identities that offer us a relationship between tan, sin, and cos. The ratio of sin and cos is always equal to tan. Similarly, the cot is the ratio of the cosine and sine ratios. Sin can alternatively be expressed as the reciprocal of cosec. Complementary identities are also crucial, as it gives the relation between sine and cos,  tan and cot, sec and cosec. Example of Complementary identity is sin(ninety-theta)= cos(theta). Similarly, many more identities such as supplementary identities, double and half angle trigonometric identities exist to assist us in solving challenges. Identities simplify our problem-solving efforts. All of them must be understood and learned to solve problems efficiently.

 

Trigonometry is a concept with numerous real-world applications. It is critical to comprehend it completely. This will assist kids in not just excelling academically, but also in solving real-life problems using these concepts. Apart from arithmetic, its concepts are employed in a variety of other fields. As a result, every student must have a thorough understanding of the subject.

 

We attempted to explore trigonometric ratios and also about trig identities in-depth in the preceding post. This will benefit not only students but everyone who wants to study trigonometry. Nowadays, there are numerous online venues where students can readily grasp these topics. However, it is recommended that youngsters learn from a few of the top online platforms, as incorrect information may be disseminated on some of the cheaper sites. There are a few excellent systems, such as Cuemath, that give us the most up-to-date information. Cuemath has already taught a large number of students a number of important ideas. Every student should participate in such platforms and get the best out of them.